Curves and Arc Length

George E. Hrabovsky

MAST

Rocky Wenz

MAST

James Firmiss

MAST

Dianna Hrabovsky

MAST

Introduction

Last time we began to explore Mathematica functionality towards a lofting application. This allowed us to establish surface representations using Delauney Trinagulations. Today we need to establish the principles of curvature leading—hopefully—to a capability to produce interpolated curves instead of the lines of the triangulation. This requires some differential geometry.

Curves

We can think of a curve as a function x of some variable that changes continuously t, thus we have a curve x(t). In more than one dimension, this is a vector, .

Arc Length

The length of a curve, s, is also a function of t, s(t),

Equation (1)

Now lets do some examples. We will make a list of interesting curves, plot the curves, and then calculate their arc lengths.

Sine curve,

Cosine Curve

Logarithmic Curve

Tangent Curve

More Sines

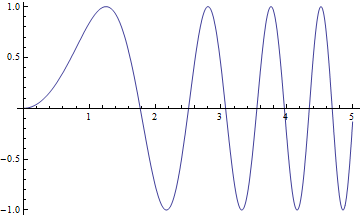
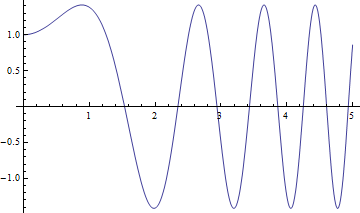
Circle

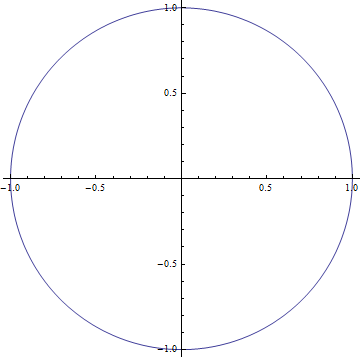
Ellipse

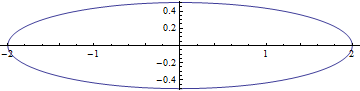
Logarithmic Spiral

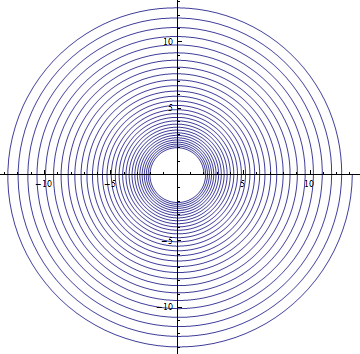
Cycloid

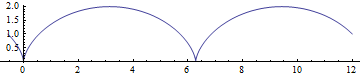
Other Trig

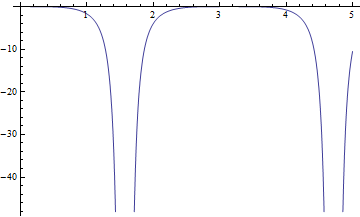
Lemniscates of Bernoulli

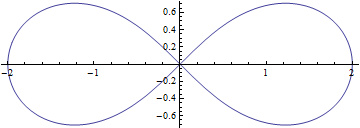
References

[1] Martin M. Lipschutz, (1969), Differential Geometry, McGraw-Hill Book Company, part of the famed Schaum’s Outline series.

[2] Alfred Gray, (1998), Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd Ed. CRC Press.

Created with Wolfram Mathematica 8.0