Complex Numbers

George E. Hrabovsky

MAST

Introduction

Complex numbers are vital to performing many calculations in physics. I hope this overview helps.

Imaginary Numbers

When we take the square of a number, the answer is always positive. It matters not that the base is negative. Thus, when we take the root of a positive number, the answer must almost always be in the form of a pair, a positive number and a negative number.

What happens if the square is a negative, number? We cleverly choose the symbol i to represent this case,

or

The symbol i is what we call the imaginary unit and any product of a real number with the imaginary unit is called an imaginary number. In engineering, the imaginary unit is often given the symbol j.

Exercise CN-1: How would we evaluate ?

Exercise CN-2: What are the first four powers of i?

Complex Numbers

One way of defining a complex number, z, is to say it is the sum of a real number, say x, and an imaginary number, say i y,

This is called the Cartesian form.

When we replace i by -i, we have the complex conjugate of z, and we write this .

In Mathematica we can find the complex conjugate of an expression by using the command Conjugate[].

Exercise CN-3: When is a complex number equal to its complex conjugate?

Exercise CN-4: How do complex numbers come into play with quadratic equations?

We can think of x as being the real part of the complex number, z. Then y would be the imaginary part. In this way we can also think of a complex number as an ordered pair of real numbers, z=(x,y). In Mathematica we can find the real part of z by using the command Re[z], and the imaginary part by Im[z].

Operations with Complex Numbers

What operations can we perform with complex numbers? Let’s say we have two complex numbers,

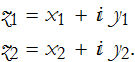
then their sum is

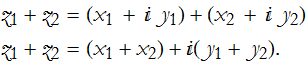
Exercise CN-5: How do subtract complex numbers?

The product of two complex numbers is similar to how we multiply two polynomials,

Exercise CN-6: What is ?

The quotient of two complex numbers is,

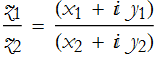
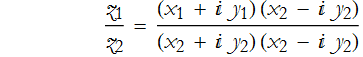
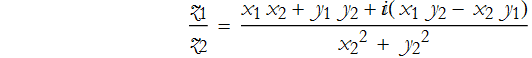
The Complex Number Plane and Argand Diagrams

We can represent complex numbers graphically. The process for this is identical to the way we represent points on the Cartesian plane. The real part is located on the horizontal axis, and the imaginary the vertical. Thus a point defined by z=x + i y and its complex conjugate are represented in Figure CN-1.

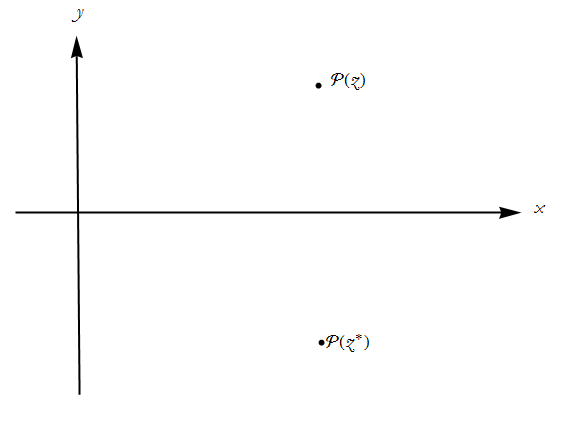
Figure CN-1: The Argand Diagram for a complex number and its conjugate.

This representation is called an Argand Diagram, named for Jean-Robert Argand (1768-1822), but is really due to Caspar Wessel (1745-1818).

Complex numbers add and subtract just as if they were arrows, the prototype of vectors. You place the tip of one vector on the tail of the other.

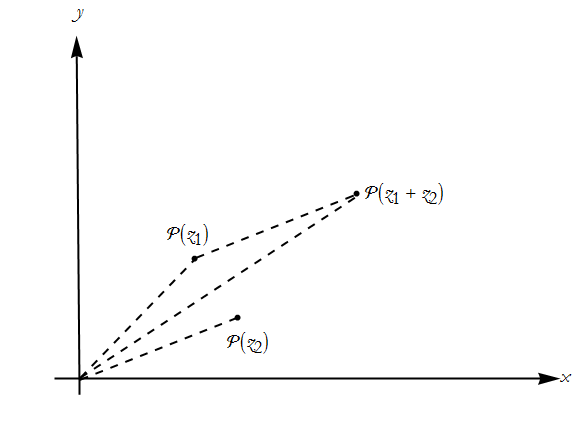
Figure CN-2: The Argand Diagram for the sum of two complex numbers.

The Polar Form of a Complex Number

We are not restricted to Cartesian coordinates. Instead of x and y, we could just as easily use distance from the origin, r, and angle from a reference line, θ. This gives us polar coordinates (see Figure CN-3).

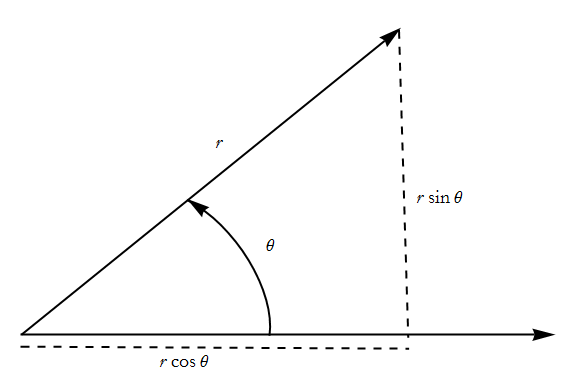
Figure CN-3: Polar coordinates.

We can see that these coordinate transformations hold,

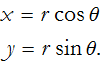
We can substitute this into (CN.3),

Exercise CN-7: What is the polar form of ?

If we know r and θ we can calculate x and y using (CN.9) above. What about the other way?

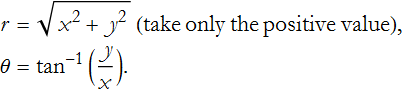
Exercise CN-8: What is ?

So we can call r the modulus, or absolute value of z, written {z}. Similarly θ is sometimes called the argument of z, written arg z. It is important to realize that if z=0, then the argument is undefined. This is because when z=0, r=0, and without any length it is not possible to define an angle, thus it can be any, or even every, possible value. This is an example of a singularity, where a value expands without limit.

For any given value of z≠0, the arc tangent is defined only to integer multiples of 2 π, since cosine and sine are periodic with the period 2 π. For this reason functions of complex numbers potentially weird. Why? Because, for any value of z the function of z might take on several values at once. This kind of function is called multiple-valued. Thus, for arc tangent function in the complex plane we could have an infinite spiral surface. Such surfaces are called branches. It is easy to see from the diagram below that an arrow drawn from a point on the bottom plane (the complex plane) would intersect each branch on the way up.

We can, however, choose one such spiral surface as representative given some criterion (in our case the integer that we multiply would be 1), this surface is then called the principal branch or principal sheet. The corresponding value of the function is then called the principal value.

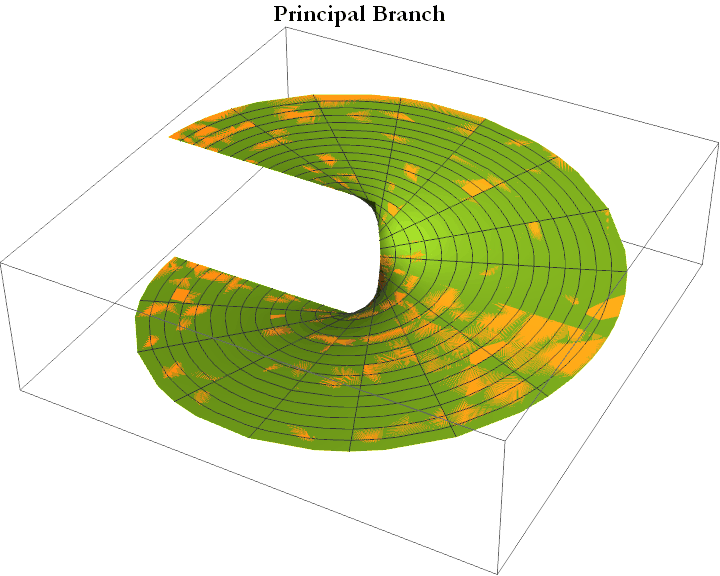
The principal value of arg z, denoted Arg z, is defined for the interval -π<Arg z≤π. Why? The tangent has the period π.

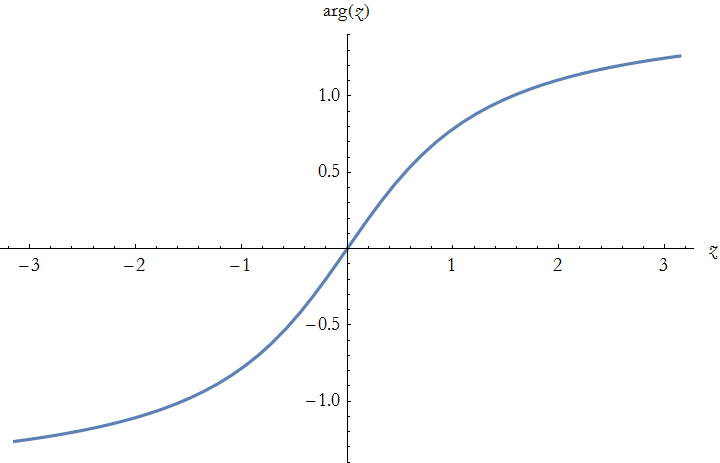
Given that (CN.9) holds, then

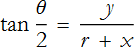
then, by definition

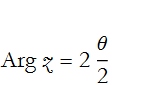
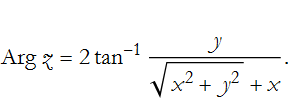
For a real value of z not equal to 0, Arg z=0, since there is no imaginary part.

Exercise CN-9: What is the polar form and arguments for z=1 + i?

The Exponential Form of Complex Numbers

We can also write complex number in a form we will see a lot in physics,

If we expand the exponential function in a power series using Mathematica, we get the first five terms

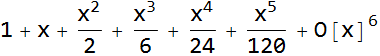
If we replace x by i θ we get

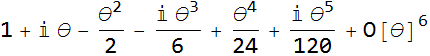
We have a polar form, given by (CN.10) z = r(cos θ + i sin θ), so let’s expand these

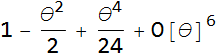
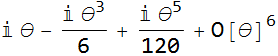
If we sum these,

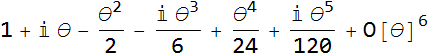
we see that this is the same as the series expansion of . Thus we can write,

This is known as Euler’s formula.

Click here to go back to the quantum mechanics page.

Click here to go back to our home page.